栈 (Stack)

基本概念

Define

堆栈（stack）又称为栈或堆叠，是计算机科学中的一种抽象资料类型，只允许在有序的线性资料集合的一端（称为堆栈顶端，top）进行加入数据（push）和移除数据（pop）的运算。因而按照后进先出（LIFO, Last In First Out）的原理运作，堆栈常用一维数组或链接串列来实现。常与另一种有序的线性资料集合队列相提并论。

Basic

• InitStack（&S）：初始化空栈S

• StackEmpty（S）：判断一个栈是否为空

• Push（&S，x）：进栈，若栈未满，则将x加入使之成为新栈顶

• Pop（&S，&x）：出栈，若栈非空，则将栈顶元素，并用x返回

• GetTop(S，&x)：读栈顶元素，若栈顶元素非空，则用x返回栈顶元素

• DestroyStack(&S)：销毁栈，并释放栈S占用的存储空间

栈的顺序存储结构

顺序栈的实现

存储结构

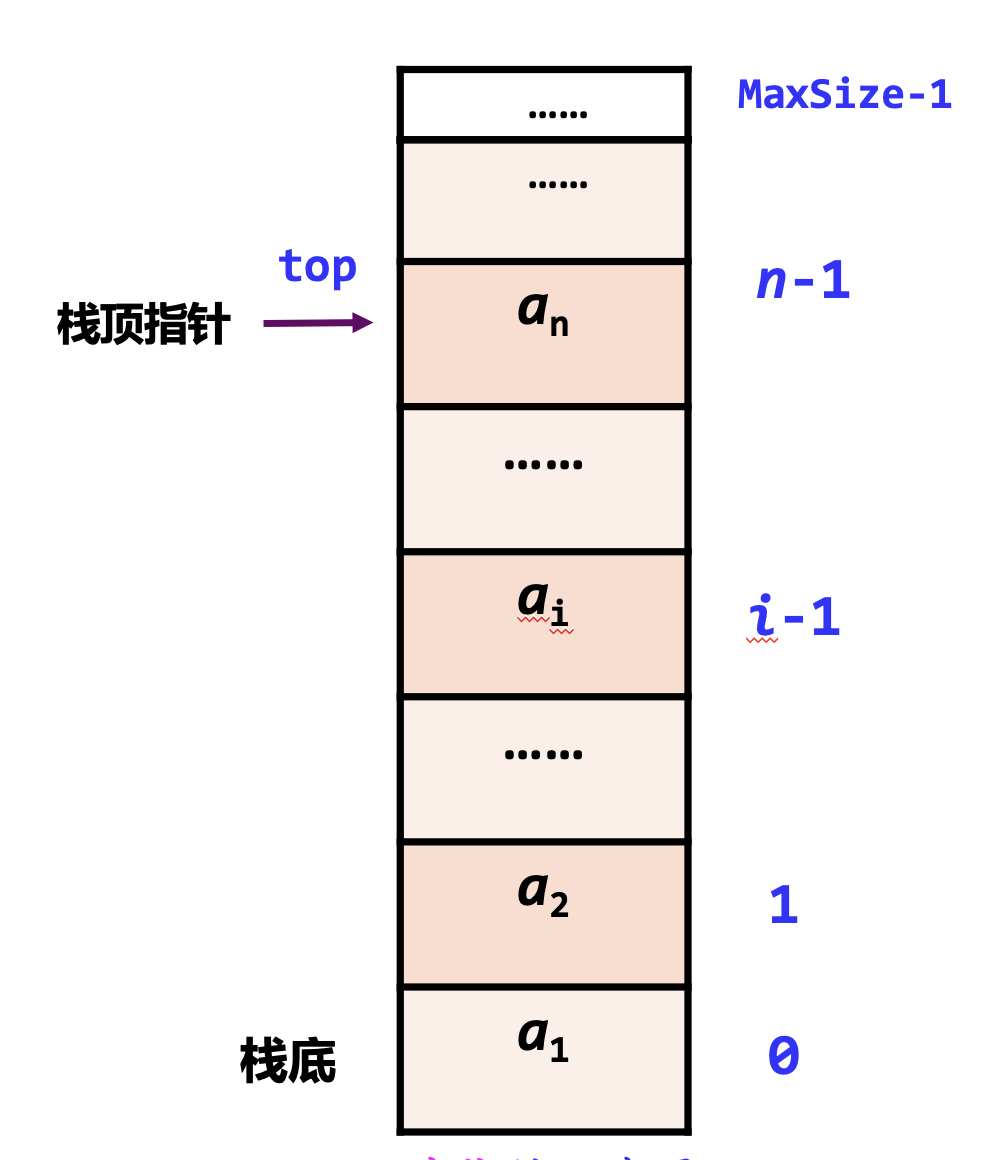
  采用顺序存储的栈称为顺序栈，它是利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶的位置。

  栈的顺序存储类型可以用以下表示：

#define MAXSIZE 100            //栈中元素的最大个数
typedef struct {
    ElemType data[MAXSIZE];    //存放栈中元素
    int top;                //栈顶指针
} SqStack;

  栈顶指针：S.top，初始时设置S.top = -1；栈顶元素：S.data[S.top]；

  进栈操作：栈不满时，栈指针加1，再送值到栈顶元素

  出栈操作：栈非空时，先去栈顶元素值，再将栈顶指针减1

  栈空条件：S.top == -1

  栈满条件：S.top == MAXSIZE - 1

  栈长：S.top + 1

顺序栈的基本运算

初始化

void InitStack(SqStack& S){
    S.top = -1;                //初始化栈顶指针
}

判栈空

bool StackEmpty(SqStack& S){
    if( S.top == -1){
        return true;
    }
    return false;
}

进栈

bool Push(SqStack& S, ElemType x){
    if( S.top == MAXSIZE - 1 ){    //栈满，报错
        return false;        
    }
    S.top ++ ;                    //栈顶指针加1
    S.data[S.top] = x;            //入栈
    return true;
}

出栈

bool Pop(SqStack& S, ElemType& x){
    if( S.top == -1 ){            //栈空，报错
        return false;
    }
    x = S.data[S.top];
    S.top --;
    return true;
}

读栈顶元素

bool GetTop(SqStack& S,ElemType& x){
    if( S.top == -1 ){            //栈空，报错
        return false;
    }
    x = S.data[S.top];
    return true;
}

共享栈

  利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数据空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。

  两个栈的栈顶指针都指向栈顶元素，top1 = -1 时，stack1 为空，top2 = MAXSIZE - 1 时，stack2 为空；仅当两个栈顶指针相邻（top1 - top2 == 1)时，判断栈满。当stack1进栈时top1先加1再赋值，stack2进栈时top2先减1再赋值；出栈正好相反。

  共享栈是为了更有效地利用存储空间，两个栈的空间正好互相调节，只有在整个存储空间被占满时才发生上溢。存取数据的时间复杂度均为O(1)，所以对存取效率没有什么影响。

栈的链式存储结构

  采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头结点，top指向栈顶元素

  链栈的存储类型可描述为:

typedef struct LinkNode{
    ElemType data;
    struct LinkNode* next;
}LinkNode, *LinkStack;