数据表示方法
A.数据格式
1.定点数的表示方法
定点数:小数点位置固定不变
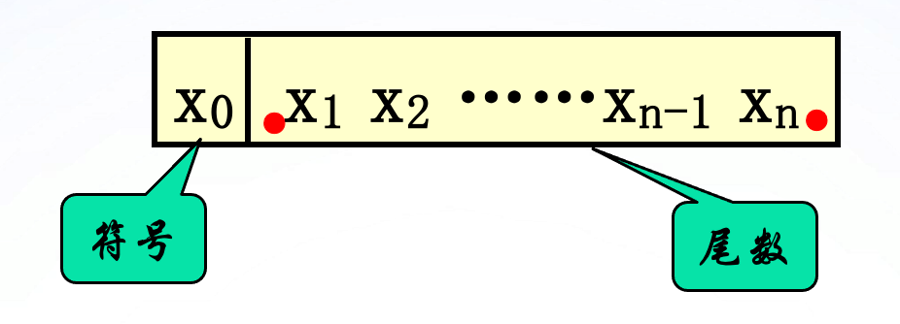
表示范围:
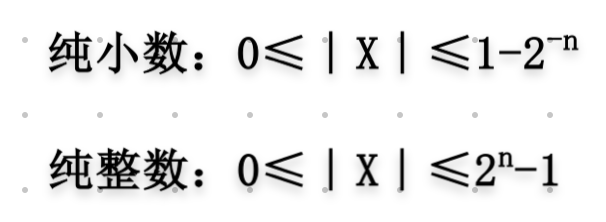
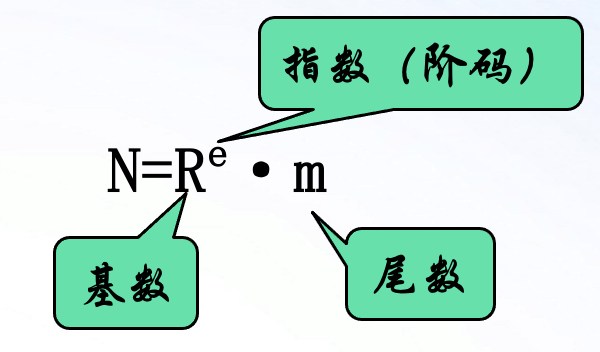
2.浮点数的表示方法
浮点数:小数点位置随比例因子的不同而在一定范围内可以自由浮动
3.十进制数串的表示方法
字符串形式(非压缩型BCD码): 一个字节保存一位
压缩的十进制数串形式(压缩型BCD码): 一个字节保存两位
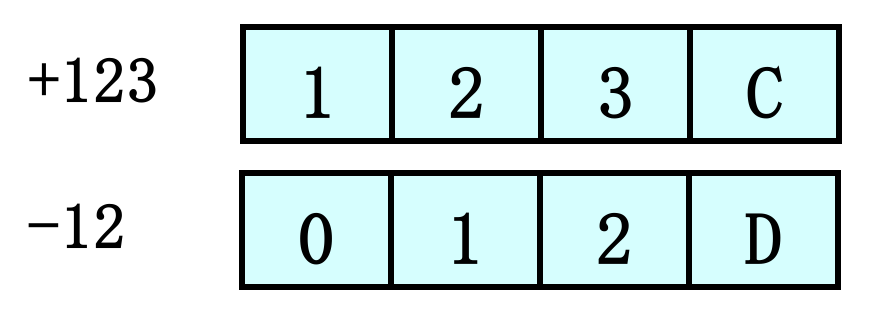
符号位:用四位编码中的六种冗余状态表示, 如用12(C)表示正号,13(D)表示负号
B.数的机器码表示
真值: 一般书写的数
机器数: 机器中把符号位和数值一起用编码表示的数
原码表示法
正数第一位为0,负数第一位为1。(如果是纯小数,则个位为符号位)
原码有两个0,以8位二进制数为例:
[+0] = 00000000[-0] = 10000000
原码表示法简单明了,易于和真值转换,但是加法运算复杂(因为需要考虑第一位的正负而不能直接把8位数相加)
反码表示法
正数的反码和原码一样,负数的反码为原码二进制取反但是符号位仍然是1,也就是说取反操作不对符号位生效
0的反码:
[+0] = 00000000[-0] = 11111111
补码表示法
正数的补码和原码一样,负数的补码相当于反码+1
补码的原理:在数的长度一定时,可以使用补码来代替负数进行加减法。即计算0111+(-0011)和计算0111+1101的结果分别为0100和10100(舍弃首位1,结果相同)
0的补码:
[+0] = 00000000[-0] = 00000000
使用补码可以把减法运算变成加法运算
如果使用原码,一个正数加一个负数不能直接把两个数的原码相加得到结果。如果使用补码,一个正数的补码加一个负数补码可以直接带上符号相加,得到的就是结果的补码
补码的补码等于自身
移码表示法
通常用来表示浮点数的阶码
移码把真值向右移动变成了非负数,即把n-1位真值(一位符号位)加上2的n次方得到移码
以6位移码举例
[+10101] = 1000000 + 10101 = 1,10101[-10101] = 1000000 + (-10101) = 0,10101
可以看到,移码使用了一个逗号(不是小数点)把第一位分离了出来,显然第一位为1时是非负数,为0时是负数
Quiz:
设机器字长16位,定点整数表示,尾数15位,数符1位,问原码、补码的表示范围分别是多少?
C.字符与字符串的表示
按照 IEEE754 的标准,有32位浮点数和64位浮点数的标准格式
IEEE754 的标准中对32位浮点数N的定义: 若E=255且M<>0,则N=NaN(无定义数据) 若E=255且M=0,则N=(-1)S∞(正负无穷) 若E=0且M=0,则N=(-1)S0(正负零) 若0<E<255,则N=(-1)S×(1.M)×2E-127(规格化数) 若E=0且M<>0,则N=(-1)S×(0.M)×2-126(非规格化数)
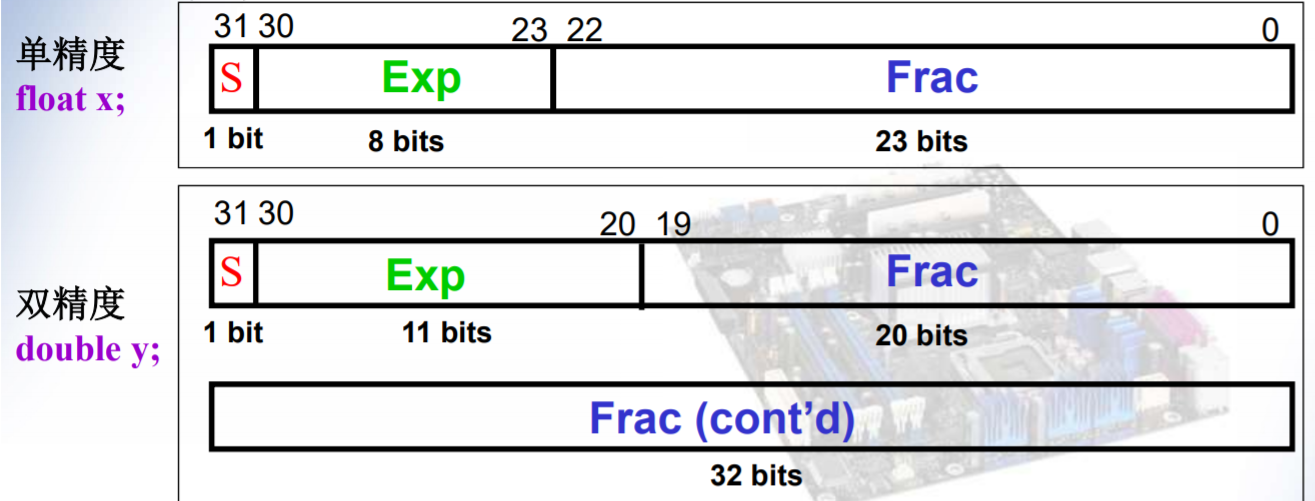
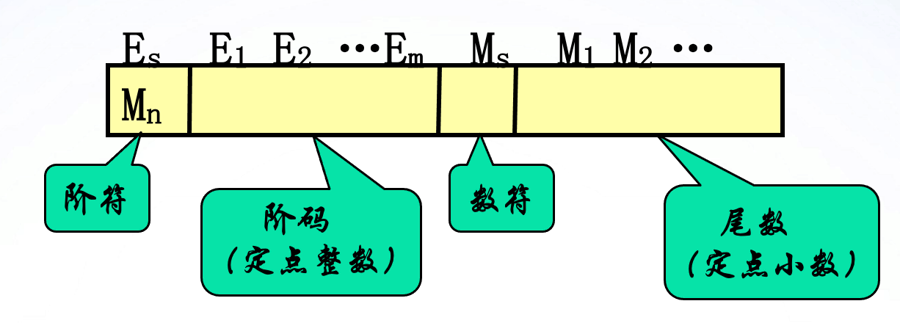
在机器中从左向右分为三个部分
S
1位
浮点数的符号位,0表示正数,1表示负数
Exp
阶码,用移码表示
float为8位,double为11位
Bias偏移量,float为127(2^7-1),double为1023(2^10-1)
Frac
小数字段,用原码表示
float为23位,double为20位
小数点在尾域的最前面。规格化数中尾数
M=1+Frac(即隐含最高位的1,提升精度,非规格化数中没有这个规则)关于移码表示的阶码:
最小的阶为00…001
最大的阶为11…110
阶码为全0与全1被用来表示其他数
基本思想:
以2.13*10^19为例,2.13为尾数,10为基数,19为阶
尾数常用原码或补码表示。尾数的有效数字位数决定了浮点数的精度
阶为定点整数,常用移码或补码表示。阶码决定了浮点数的表示范围
规格化尾数规格化形式:尾数为纯小数且最高位必须为1(原码表示时为1,如果是补码或反码的负数则最高位为0),个位表示符号,0为正1为负 每个小数都可以转换成一个唯一的规格化数
example:
若浮点数x的754标准存储格式为(41360000)16,求其浮点数的十进制数值。
二进制表达: 0 100 0001 0 011 0110 0000 0000 0000 0000
求E: e=E-127=10000010-01111111=00000011=3(10)
1.M=1.011 0110 0000 0000 0000 0000 =1.011011
X=(-1)^S× (1.M)× 2^e = = +(1.011011)×2^3 = 11.375(10) 👏
特例:
x=-1/2=-0.100...0的补码1.100...0在补码中不是规格化数x=-1的补码1.00...00是规格化数
D.校验码
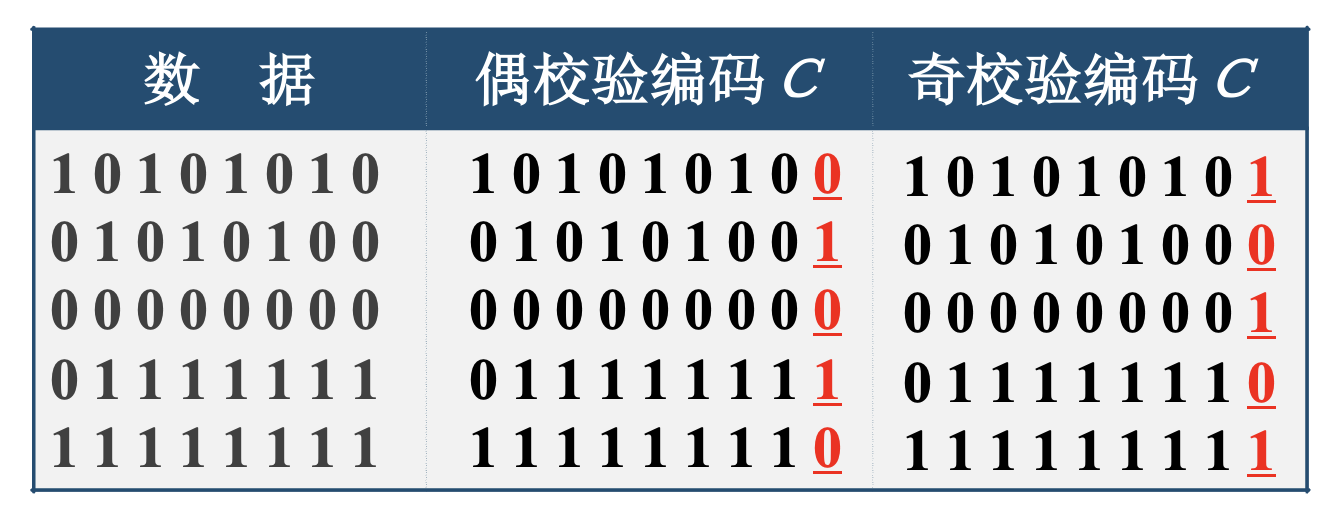
奇偶校验码:加一个校验位,使整个数据中1的个数保证为奇(偶)数个。
0110110 奇校验位为1,偶校验位为0 设X=X0X1X2……Xn-1,则 偶校验位C=X0⊕X1⊕X2⊕ ……⊕Xn-1 发送时,数据为X0X1X2……Xn-1C 接收时,数据为X0′X1′X2′……Xn-1′C′ 接收校验F= X0′⊕X1′⊕X2′⊕……⊕Xn-1′⊕C ′ 若F=1,则接收信息有错 优点:实现简单 缺点:只能检测奇数个错误
Last updated
